Snell's law
Definition
Snell's Law, also known as the Law of Refraction, describes how the direction of a wave changes as it passes from one medium to another with a different refractive index. It is fundamental to understanding phenomena such as the refraction of light when it passes through water, glass, or any other transparent material.
The mathematical expression of Snell's Law is:
$$n_{1} \sin (\theta_{1}) = n_{2} \sin (\theta_{2})$$
or taking into account the speed of light in each medium:
$$\frac{\sin\theta_{1}}{\sin\theta_{2}} = \frac{v_{1}}{v_{2}} = \frac{n_{2}}{n_{1}}$$
where:
- \(\theta_{1}\) is the angle of incidence in the first medium
- \(\theta_{2}\) is the angle of refraction in the second medium
- \(v_{1}\) is the speed of light in the first medium
- \(v_{2}\) is the speed of light in the second medium
- \(n_{1}\) is the refractive index of the first medium
- \(n_{2}\) is the refractive index of the second medium
Key Concepts
- The refractive index \((n)\) of a medium is defined as the ratio of the speed of light in a vacuum to the speed of light in that medium: $$n = \frac{c}{v}$$
-
If light passes from a less optically dense medium to a
more optically dense one (e.g., from air to water), it
the normal \(\theta_{1} < \theta_{1}\). - If it passes from a more dense to a less dense medium, it bends away from the normal \((\theta_{2} > \theta_{1})\).
Applications
- Design of lenses and optical systems.
- Explanation of phenomena such as mirages or the apparent bending of submerged objects.
- Fiber-optic telecommunications.
Simulation
Move the green slider to change angle of incidence, move the black sliders to change the refractive indices. Being \(n_{1}\) that of the upper part and \(n_{2}\) that of the lower part.
Explanation
To find out the optimal path of light, we must first assume that \( A=(a,b) \) lies over the \(x\)-axis and that \( B=(c,d) \) lies below the \(x\)-axis, as depicted in the image below:
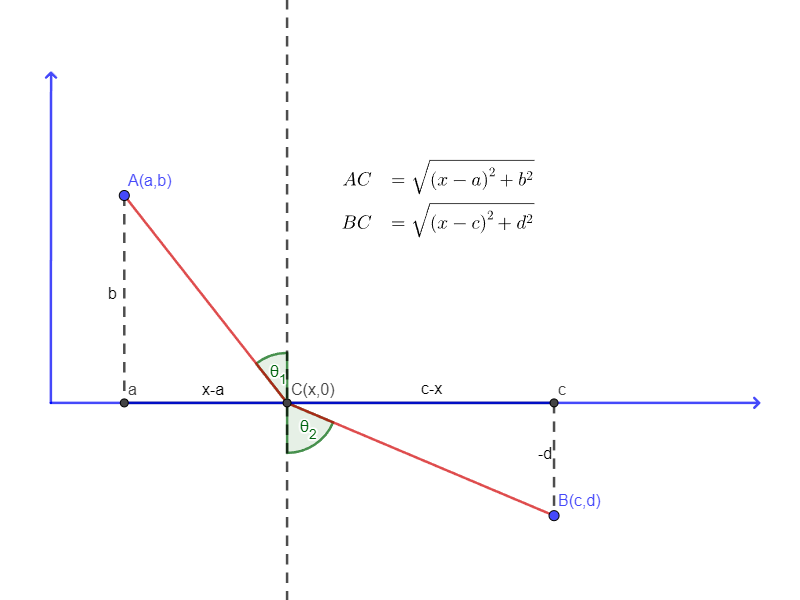
To minimize the travel time from \(A\) to \(B\), we need to find the point \(C=(x,0)\) on the \(x\)-axis. We assume that the velocity on the \(x\)-axis is \(v_{1}\), while below the \(x\)-axis it is \(v_{2}\). Since we can derive time from velocity, we seek the point \(C\) that satisfies this condition.
$$\mathrm{time = \frac{distance}{velocity}},$$
so the travel time is
$$T\left( x \right) = \frac{\sqrt{\left(x - a\right)^{2} + b^{2}}}{v_{1}} + \frac{\sqrt{\left(x - c\right)^{2} + d^{2}}}{v_{2}}.$$
If we calculate the derivative and set it equal to \( 0 \), we have
$$\frac{\frac{1}{2}\left[ \left( x - a \right)^{2} + b^{2} \right]^{-1/2} \cdot 2\left( x - a \right)}{v_{1}} + \frac{\frac{1}{2}\left[ \left( x - c \right)^{2} + d^{2} \right]^{-1/2} \cdot 2\left( x - c \right)}{v_{2}} = 0.$$
Which can be rewritten as
$$\frac{x - a}{v_{1}\sqrt{\left( x - a \right)^{2} + b^{2}}} + \frac{x - c}{v_{2}\sqrt{\left( x - c \right)^{2} + d^{2}}} = 0.$$
But we can notice in the previous image
$$ \begin{split} \sin\theta_{1} &= \frac{x - a}{\sqrt{\left(x - a\right)^{2} + b^{2}}} \\ \sin\theta_{2} &= \frac{c - x}{\sqrt{\left(x - c\right)^{2} + d^{2}}} \end{split} $$
that way we can rewrite the above equation as
$$\frac{\sin\theta_{1}}{v_{1}} - \frac{\sin\theta_{2}}{v_{2}} = 0$$
equivalently it is
$$\frac{\sin\theta_{1}}{\sin\theta_{2}} = \frac{v_{1}}{v_{2}},$$
which is the Snell's Law.